문제
https://www.acmicpc.net/problem/1074
풀이
- 사용한 알고리즘
분할 정복 알고리즘 > 이진 탐색으로 푸는 문제다. (2^N x 2^N)배열에서의 답을 구하기 위해 (2^(N-1) x 2^(N-1))배열, 그리고 (2^(N-2) x 2^(N-2))배열, ... 과 같이 작은 형태의 문제로 나누어 해를 구하다 보면 최종적으로 원래 문제의 답이 구해지는 형태이고, 나눠진 작은 문제들에서도 배열을 Z자 형태로 방문하는 행위가 똑같이 반복되고 있기 때문이다. 문제 풀이를 완전히 이해하고 난 후 다시 읽으면 무슨 말인지 한 번에 와닿을 것이다.
큰 문제를 작은 문제로 나눠서 푼다는 점에서 동적 계획법(DP)을 떠올리기 쉬운데, 이 문제의 경우에는 작은 문제의 해답을 저장해뒀다가 다시 사용하는 과정이 필요없으므로 동적 계획법에 해당되지 않는다. 상위 문제와 하위 문제의 해답 찾는 과정이 긴밀하게 연관되어있지 않고 독립적으로 수행된다. - 문제 풀이

먼저 전체적인 동작을 이해해보자.
배열을 Z형태로 방문함 -> Z형태를 그리는 동시에 더 큰 Z형태로 방문함 -> 반복

반복되는 문제 중 '가장 작은 문제'가 뭔지 찾아보자. Z형태로 움직이며 1씩 증가하는 동작이다.

그 뒤로도 이 문제와 같은 형태가 계속 반복된다. 그렇다면 문제가 반복되면서 변하는 것이 무엇인지 생각해보자.
가장 작은 문제가 4번 수행되며 큰 Z를 그릴 때, 가장 첫 번째 값이 4의 배수로 늘어나고 있다.

N이 3으로 늘어났을 때도 똑같은 아이디어를 적용해보자.
앞서 구한 부분이 4번 수행되며 큰 Z를 그릴 때, 가장 첫 번째 값이 16의 배수로 늘어나고 있다.
아무튼 문제에서 제시한부분을 이해했고, 그에 따른 규칙도 찾았다. 그런데 우리는 입력받은 위치를 찾은 후 그 위치에 있는 값까지 구해야 한다. 앞서 찾은 규칙을 적용해보면 다음과 같이 생각할 수 있다.
(1, 3)의 위치 찾는 법 :
8*8 배열에서 크게 Z를 그리며 동작이 진행된다고 보았을 때, 크게 4*4로 이루어진 네 구역으로 나눌 수 있다. 그 중 첫 번째 구역에 (1, 3)이 있다. -> 찾은 첫 번째 구역 4*4배열에서 동일하게 2*2로 이루어진 네 구역 중 세 번째 구역에 (1, 3)이 있다. -> 찾은 세 번째 구역 2*2배열에서 네 번째 구역에 (1, 3)이 있다.
(1, 3)의 값 찾는 법 :
8*8배열의 첫 번째 구역의 첫 번째 값 = 0
4*4배열의 세 번째 구역의 첫 번째 값 = 8
2*2배열의 네 번째 구역의 첫 번째 값 = 3
따라서 0+8+3 = 11
즉, Z형태를 만날 때마다 상하좌우 네 섹션 중 어디에 내가 찾고자 하는 값이 있는지 판단하여, 그 섹션의 가장 첫 번째 값을 누적하는 행위를 답이 구해질 때까지 반복하면 된다. (여기서 반복 횟수는 몇 개의 간단한 예제를 손코딩해보면 N번이라는 것을 알 수 있다.)
좀 더 자세한 풀이>>..
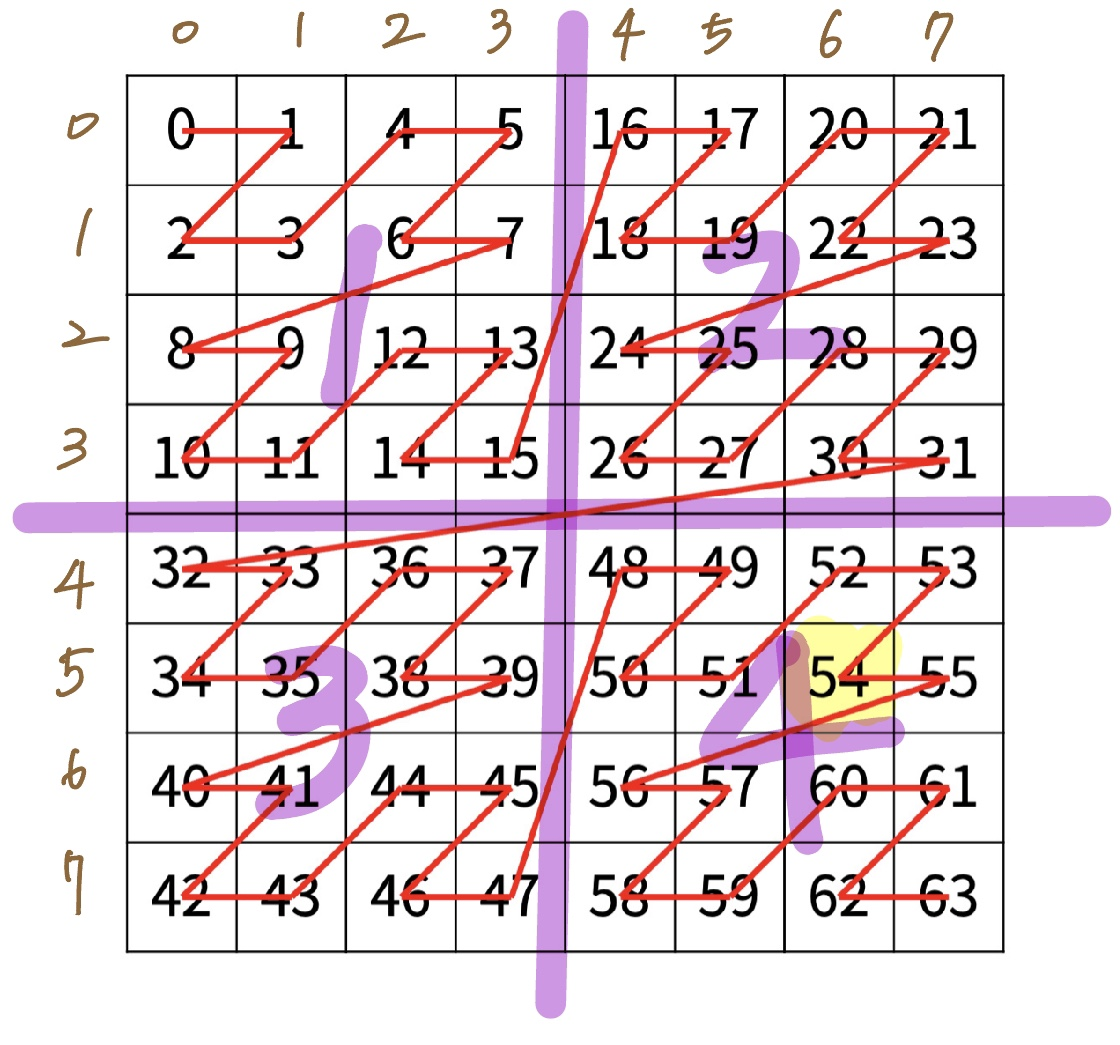
8*8 배열에서 방금 문제를 구한 방식과 똑같은 풀이방식을 적용해 답을 구해보자.
1) 배열을 십자로 네 등분 하고
2) 구하고자 하는 위치가 네 곳 중 어디에 있는지 구한 후
3) 위치 별로 배열의 가장 첫 번째에 위치한 값을 더하여 해를 구할 수 있다.
위 그림에서 표현된 것과 같이 Z형태 순서대로 위치가 1, 2, 3, 4라고 하면
(5, 6)은 8*8 배열의 위치 4에 존재하므로 먼저 48을 누적한다.
(8*8 배열의 위치4의 첫 번째 값은 48)

그리고 위치 4로 범위를 좁혀서 같은 방법을 적용하면
(5, 6)은 4*4배열의 위치 2에 존재하므로 4를 누적한다.
(4*4 배열의 위치2의 첫 번째 값은 4)

마지막으로 위치 2로 범위를 좁혀서 같은 방법을 적용하면
(5, 6)은 2*2 배열의 위치 3에 존재하므로 2를 누적한다.
(2*2 배열의 위치3의 첫 번째 값은 2)
따라서 답은 48+4+2=54가 된다.
왜 각 섹션의 첫 번째 값을 누적하는가? 2*2배열에서 네 번째에 있는 값을 구할 때는 0에 3을 더해주면 되는 것과 같은 원리이다. 2*2배열은 섹션별로 1씩 증가해서 3을 더해줬을 뿐이다. 8*8배열은 섹션별로 16씩 증가하니까 16*3을 더해줘야 한다.
코드
import java.io.*;
import java.util.*;
public class Main{
static int length; //배열 한 변의 길이
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw =new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int r = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
bw.write(recursion(N, r, c) + "");
bw.close();
}
static int find(int N, int r, int c){
//섹션을 찾는 함수 (왼쪽위부터 차례로 1234로 가정)
//N이 주어지면 NxN 크기의 배열을 4섹션으로 나눈 후,
//섹션 찾기를 N번 반복 -> 각각 (--)(-+)(+-)(++)으로 판단
int a = (r+1) - length/2;
int b = (c+1) - length/2;
if(a <= 0 && b <= 0) return 1;
else if(a <= 0 && b > 0) return 2;
else if(a > 0 && b <= 0) return 3;
else if(a > 0 && b > 0) return 4;
else return 0;
}
static int recursion(int N, int r, int c){
//for문을 돌며 한 번 섹션을 찾을 때마다 해당 배열의 섹션 첫 번째 값을 누적시킴
double sum = 0; //값을 누적할 변수
int P = N; //N의 값이 갱신되어야 하는데, for문 조건식에도 써야 하므로 따로 P에 복사해서 사용
//섹션 찾기를 N번 반복
for(int i=0; i<P; i++){
length = (int)Math.pow(2, N);
int section = find(N, r, c);
int first = (int)Math.pow(2, (N-1)*2); //해당 배열의 섹션 첫 번째 값
switch(section){
case 1:
//섹션1은 0을 누적
break;
case 2:
c -= length/2; //다음 for문을 돌 때 범위가 작아지므로 행, 열값도 새로 갱신
sum += first;
break;
case 3:
r -= length/2;
sum += first * 2;
break;
case 4:
r -= length/2;
c -= length/2;
sum += first * 3;
break;
default:
break;
}
N--; //배열 범위 작게 변경
}
return (int)sum;
}
}
Note
- 처음에는 배열의 한 변의 길이인 length와 그 절반값을 (int)Math.pow(2, N-1)로 일일이 선언해서 풀었다. 이 부분을 개선하니 메모리가 98KB 절약되었다.
- 이 문제를 통해 이진검색 알고리즘을 언제 적용해야 하는지 감이 잡혔다.
- 문제 접근 방법, 풀이 이해, DP와 이진검색 알고리즘의 차이점을 제대로 공부하는 데 생각보다 많은 시간을 할애했지만 덕분에 해당 유형과 비슷한 문제를 만났을 때 이전보다 잘 대처할 수 있게 되었다.
'BOJ' 카테고리의 다른 글
| [백준 9663번/java] N-Queen (0) | 2024.06.11 |
|---|---|
| [백준 4485번 / java] 녹색 옷 입은 애가 젤다지? (0) | 2024.05.13 |
| [백준 1463번/JAVA] 1로 만들기 (0) | 2024.04.09 |
| [백준 1003/JAVA] 피보나치 함수 (0) | 2024.03.31 |
| [백준 2839번/JAVA] 설탕 배달 (0) | 2024.03.31 |